Numération

Bien que ce sujet soit vu en beaucoup plus de détails dans le chapitre MathInfo, voici le minimum de ce qu'il faut savoir à propos de la numération binaire et hexadécimale.

Bit, byte, octet

Quelles que soient les informations et les conventions choisies pour les coder, leurs codes sont toujours transcrits en binaire car c'est techniquement plus facile à réaliser dans un ordinateur pour le traitement, le stockage et les transmissions.

Le système binaire est un système à deux états qui correspondent à une présence ou une absence de signal électrique, magnétique ou optique.

L'information élémentaire est appelée bit contraction de binary digit (chiffre binaire)

Un bit ne peut prendre que deux valeurs 0 et 1

On regroupe les bits par mots de différentes largeurs : mots de 8, 16, 32 ou 64 bits.

Les mots de 8 bits sont appelés octets ou « bytes » en anglais.

Avec un octet on peut représenter 2⁸ = 256 codes différents

Ces bits et ces octets servent à coder des informations de toutes natures.
Les systèmes informatiques doivent donc être organisés pour savoir où et de quelle nature sont les informations qu'il manipule. ( contrairement aux informations sur papier où on distingue immédiatement si ce qu'on voit est une image ou un texte)

Numérations de position

Considérons le nombre 1975. Ce nombre est un "mot" dont les caractères sont les chiffres. La valeur que l'on attribue à chaque chiffre dépend du chiffre en lui-même et de sa position.
-  le 1 vaut 1 x 1000.
-  le 9 qui suit représente des centaines, il vaut 9 x 100.
-  le 7 représente des dizaines, il vaut 7 x 10.
-  le 5 vaut 5 x 1.
Nous utilisons un système de numération de position et la base 10.

La base 10

La base 10 ou base décimale est celle que nous utilisons tous les jours.
Nous disposons de 10 chiffres (de 0 à 9) pour compter.
Après avoir compté 10 unités, nous utilisons deux chiffres pour écrire le nombre 10 :
- le 1 signifie que nous avons fait un paquet de dix unités que nous appelons dizaine,
- le 0 qui suit signifie que nous comptons les nouvelles unités dans un paquet qui pour l'instant est vide.
Le nombre de dizaines ne peut dépasser 9. Il nous faut donc un troisième chiffre pour compter dizaines par dizaines, ce "report" indique les centaines.
De droite à gauche on a donc les unités puis les dizaines, les centaines, les milliers et toutes les puissances successives de 10.

N.B. Il existe d'autres bases. Les Babyloniens utilisaient par exemple la base 60. C'est ce qui a marqué notre façon de compter les minutes et les secondes, celles pour mesurer le temps qui passe ou pour mesurer les angles.
Nos ancêtres utilisaient une base 20. Au lieu de compter par dizaines, ils comptaient par vingtaines (deux-vingt, troix-vingt, quatre-vingt ) Si le sujet vous intéresse allez voir ce site sur l'histoire des chiffres

Le poids des chiffres

Reprenons notre exemple 1975. Numérotons les positions des chiffres de doite à gauche en commençant par 0 pour la position des unités.

Le poids d'un chiffre dépend de sa position et de la base    Poids = base ^position
Voici ce que cela donne dans notre exemple :
Le poids du chiffre 1 est 10³ sa valeur est 1 x 10³ = 1 x 1000 = 1000
Le poids du chiffre 9 est 10² sa valeur est 9 x 10² = 9 x 100 = 900
Le poids du chiffre 7 est 10¹ sa valeur est 7 x 10 = 70
Le poids du chiffre 5 est 10⁰ sa valeur est 5 x 1 (car 100 = 1)

Numération binaire

La base est 2. Nous n'utilisons que deux chiffres 0 et 1.

Remarquez qu'en base 2, le chiffre 2 n'existe pas ; tout comme le chiffre 10 n'existe pas en base 10.

Il s'agit toujours d'une numération de position. De droite à gauche nous avons donc les unités puis les "deuzaines", les "quatraines", les huitaines, les seizaines, les "trentedeuzaines" etc.

Exemple : que vaut le nombre binaire 10110 ?

Le poids d'un chiffre dépend de sa position et de la base.

Poids = base ^position ici en binaire le poids = 2 ^position

On a donc ici une seizaine, une "quatraine" et une "deuzaine" soit 16 + 4 + 2 = 22

La phrase suivante restera énigmatique tant que vous n'aurez pas compris ce qui précède !

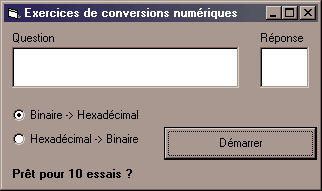
Exercez-vous avec la balance ci-dessous pour vous habituer aux poids des chiffres binaires Lancer l'exercice en cliquant sur ce bouton :   Cliquez ensuite sur les poids (ici plus bas) pour les poser sur la balance ou pour les retirer.

Entraînez-vous avec cet exercice pour vous familiariser à l’écriture des nombres en binaire. Choisissez vos poids comme vous le feriez avec une vraie balance, en commençant par les poids les plus gros pour finir en ajustant avec les plus petits. Cette méthode est la plus simple tant que le nombre à représenter est relativement petit. Ici avec 6 bits on ne pourra écrire que des nombres allant de 0 à 63. Ensuite, si les calculs mentaux ne vous font pas peur, vous trouverez ici le même exercice avec 8 bits.

Les codes binaires sont incontournables en informatique puisque l'information la plus élémentaire y est le bit ( Binary digit - chiffre binaire)

Les mots de 8 ou de 16 bits écrits en binaire sont plus lisibles si on les inscrit en laissant un espace entre les groupes de quatre bits comme ceci : 0100 0001
On a aussi avantage à représenter les zéros non significatifs pour montrer la taille des codes transcrits. Il faut remarquer d'ailleurs que ces 0 à gauche ne sont pas toujours "non significatifs". En effet, les codes binaires ne représentent pas toujours des valeurs numériques. Ce sont parfois simplement des codes qui ne représentent pas des quantités et qui n'ont pas non plus de valeur ordinale. Inutile donc de faire de l'arithmétique avec ces codes. Dans ce cas cela n'a aucun sens de vouloir les convertir en décimal et ce serait une erreur d'omettre l'écriture des zéros à gauche.

Numération hexadécimale

La base est 16. Il nous faut donc 16 chiffres, nous avons déjà les chiffres 0 à 9, ajoutons-y les caractères A, B, C, D, E et F pour représenter les "chiffres" de 10 à 15.

Remarquez qu'en base 16, le chiffre 16 n'existe pas ; tout comme le chiffre 10 n'existe pas en décimal ni le chiffre 2 en binaire.

Nous appliquons toujours les mêmes principes de la numération de position.

Le poids d'un chiffre dépend de sa position et de la base

Poids = base ^position ici en hexadécimal le poids = 16 ^position

De droite à gauche nous avons donc les unités puis les "seizaines", les "256^zaines" etc.

Exemple : que vaut le nombre hexadécimal 1A2F ?

L'addition des valeurs de ces 4 chiffres donne : 4096 + 2560 + 32 + 15 = 6703

A quoi sert l'hexadécimal ?

Les codes hexadécimaux sont bien pratiques en informatique. Ils permettent de lire les codes binaires de manière compacte et nous évitent de devoir lire de longues enfilades de 0 et de 1 qui conviennent mieux aux ordinateurs qu'aux humains.

Un groupe de quatre bits permet de former 16 combinaisons différentes. Une valeur hexadécimale correspond à chaque combinaison. L'hexadécimal c'est du binaire condensé.

Le code hexadécimal 1A2F est bien plus lisible que   0001 1010 0010 1111 en binaire